2023年 千葉県公立高校入試 数学 3 (2)
千葉県公立高校入試では証明問題が出題されます。
2023年の大問3(2)は正答率が3%以下という難問だったようです。
当塾でも質問がたくさんありました。
もちろん、それぞれの生徒さんに説明はしていますが、
ここにもまとめておきたいと思います。
問題
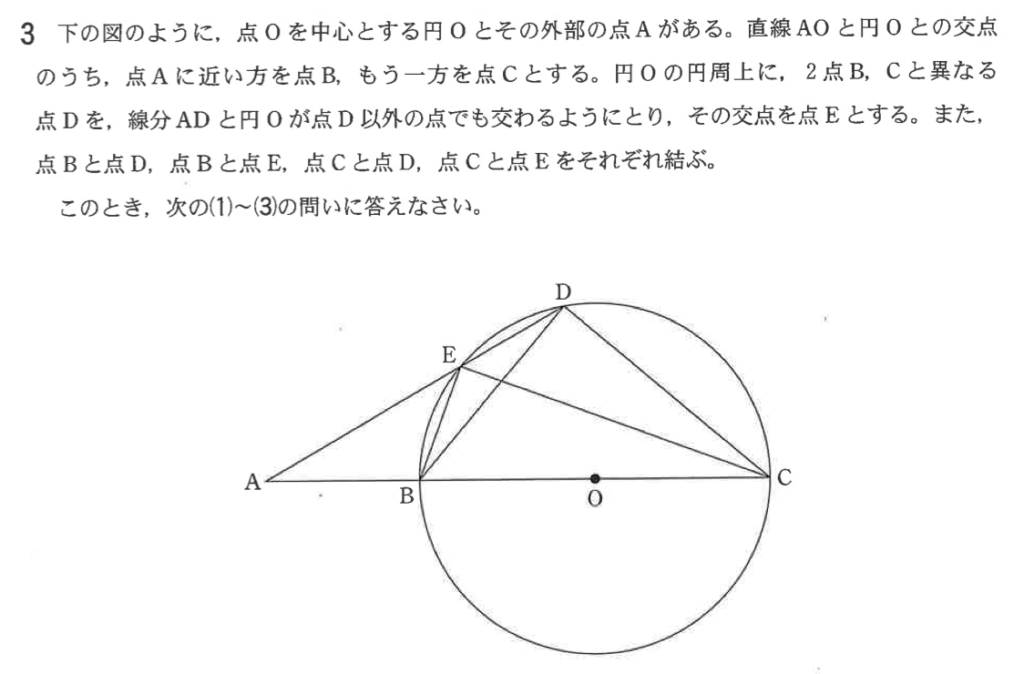
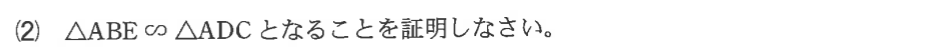
解説(解答)
まず、何をするのかを確認しましょう。
下の図を見てください。△ABE(下の図で赤で塗ったもの)と
△ADC(下の図で青で塗ったもの)が相似であることを証明するという問題です。
長さについてはほとんど情報がないので、長さの比ではなく角度で考えるのでしょう。
つまり、二つの角が等しいということを証明すればいいのです。
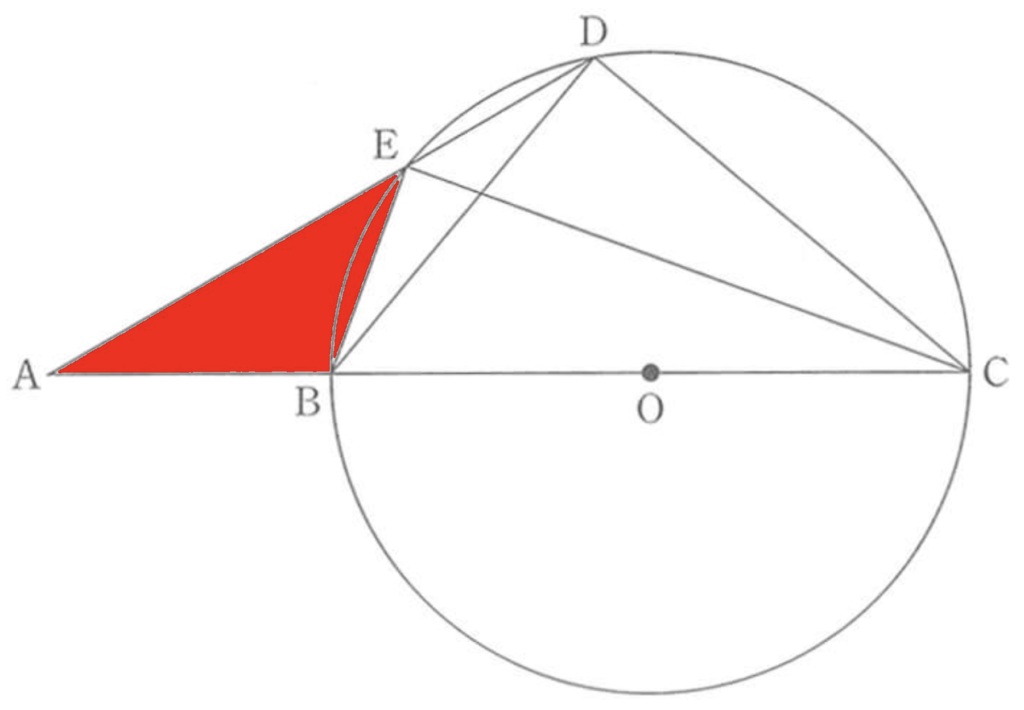
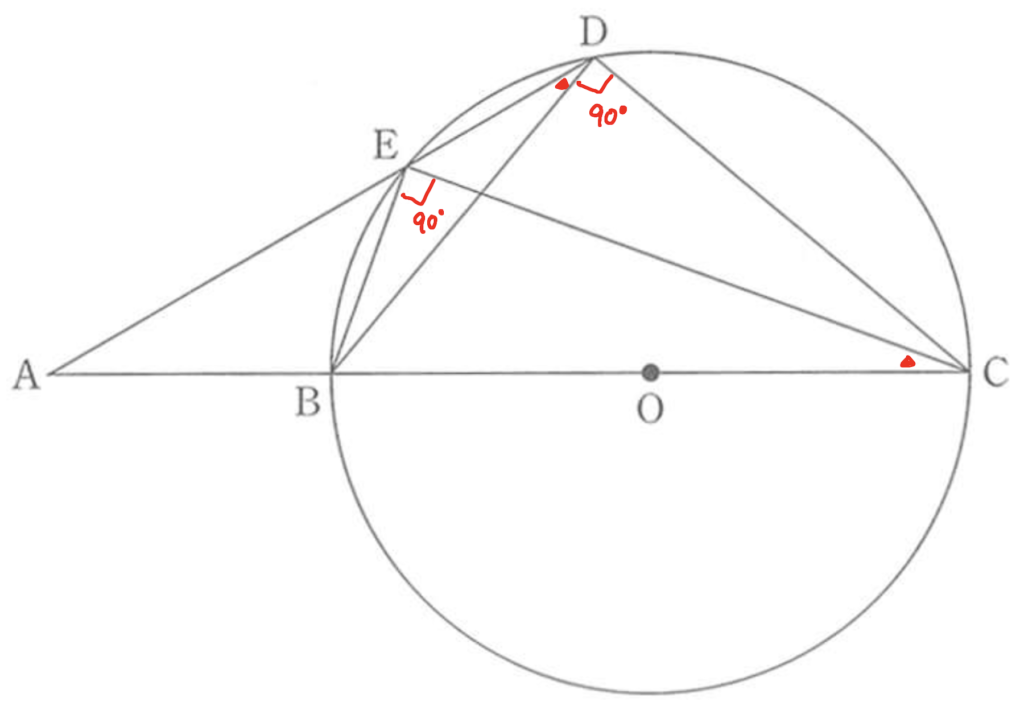
まず、上の図を見れば一目瞭然ですが、
△ABE(赤)における<BAEと
△ADC(青)における<CADは
同じ角ですから角度は等しくなります。
証明
<BAE = <CAD ・・・ ①(共通)
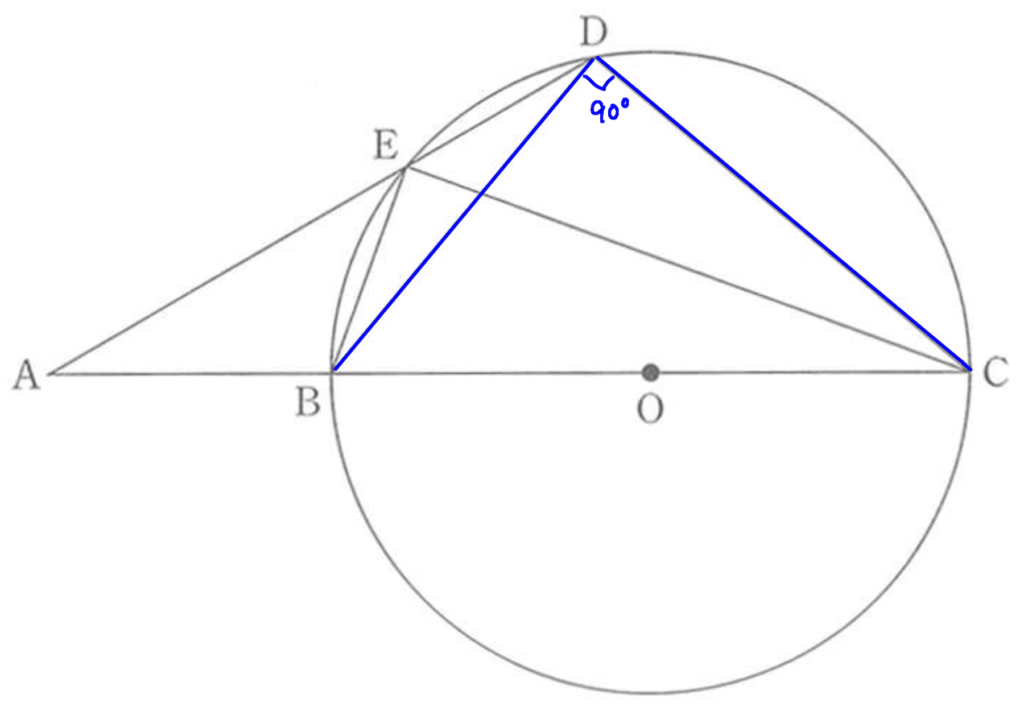
次に<BDCと<BECを見てみます。
両者とも点B、点Cを両端としています。
線分BCは円の直径です。
すると、円の直径に対する円周角ですから<BDCと<BECは直角(90°)です。
実はこれは大問3の(1)で出てきています。
今回は(1)は省略しました。
証明
<BAE = <CAD ・・・ ①(共通)
<BCDと<BECは円の直径に対する円周角なので、90° ・・・ ②
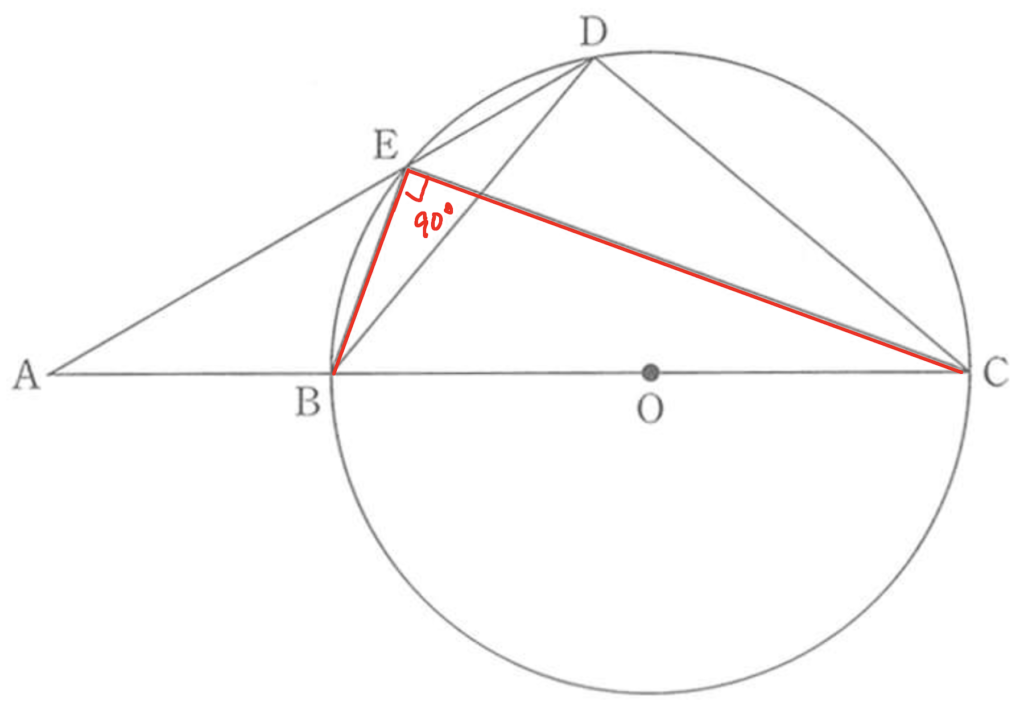
次に<EDBと<ECBを見てみます。
両者とも孤EBに対する円周角です。
ということは、何度かは分かりませんが、同じ角度ということになります。
証明
<BAE = <CAD ・・・ ①(共通)
<BCDと<BECは円の直径に対する円周角なので、90° ・・・ ②
<EDBと<ECBは孤EBに対する円周角なので角度は等しい ・・・③
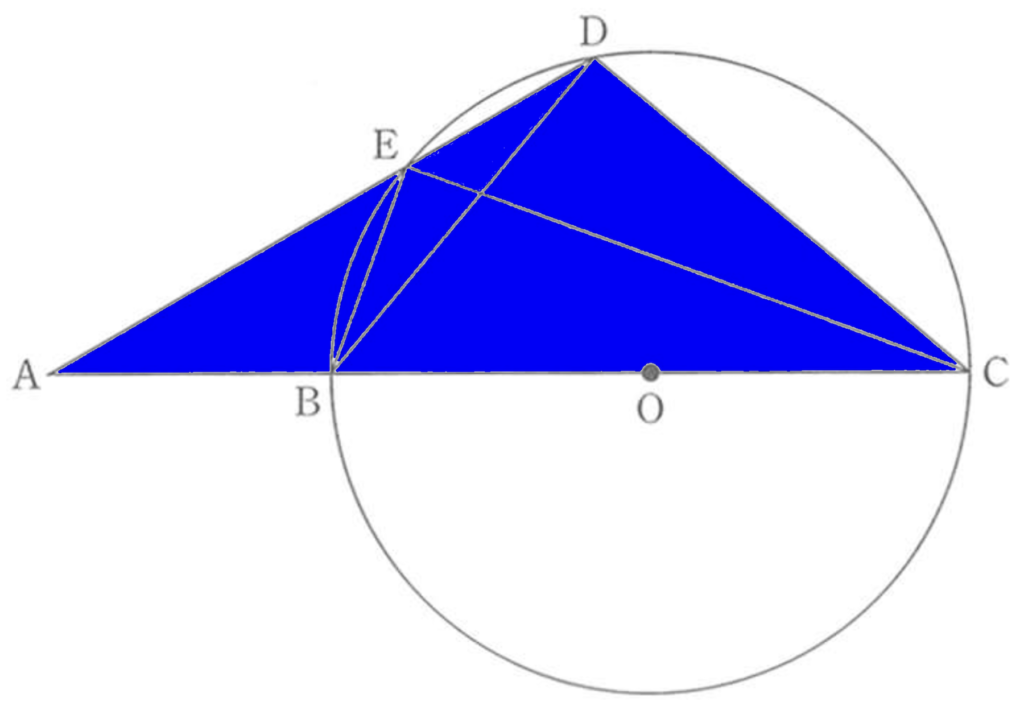
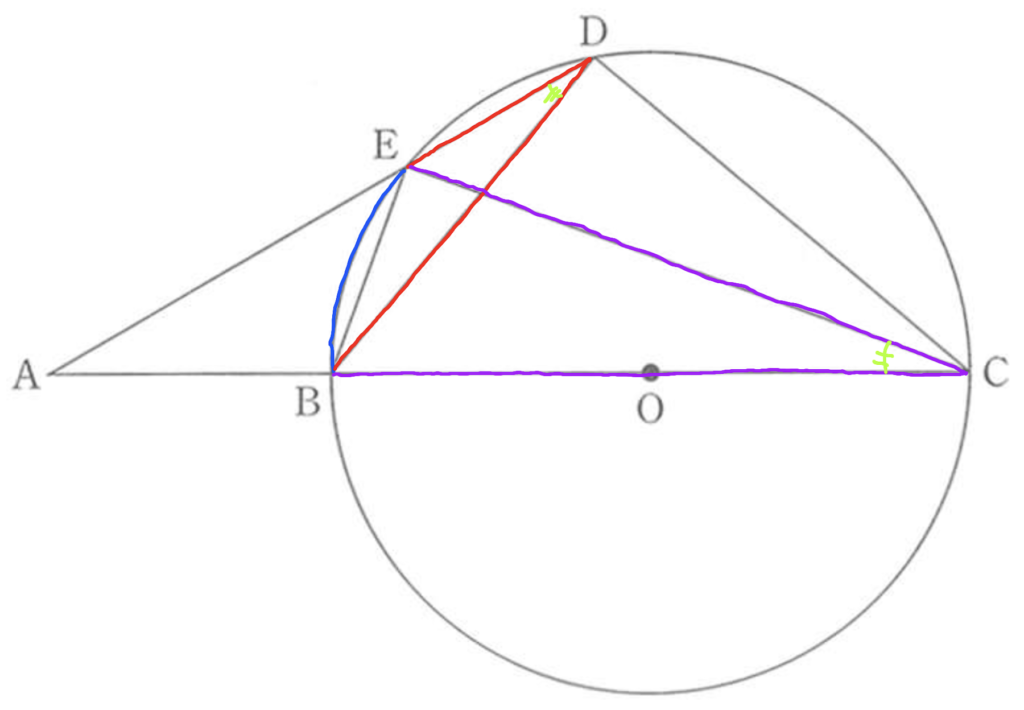
以上のことから、上の図のようなことがわかります。
△ADCにおいて、<ADCは90°+<EDBとなります。
この<EDBというのは<ECBと等しい角でした。
また、<BECは90°であることも確認しておきます。
証明
<BAE = <CAD ・・・ ①(共通)
<BCDと<BECは円の直径に対する円周角なので、90° ・・・ ②
<EDBと<ECBは孤EBに対する円周角なので角度は等しい ・・・③
②、③より
<ADC = 90° + <EDB ・・・④
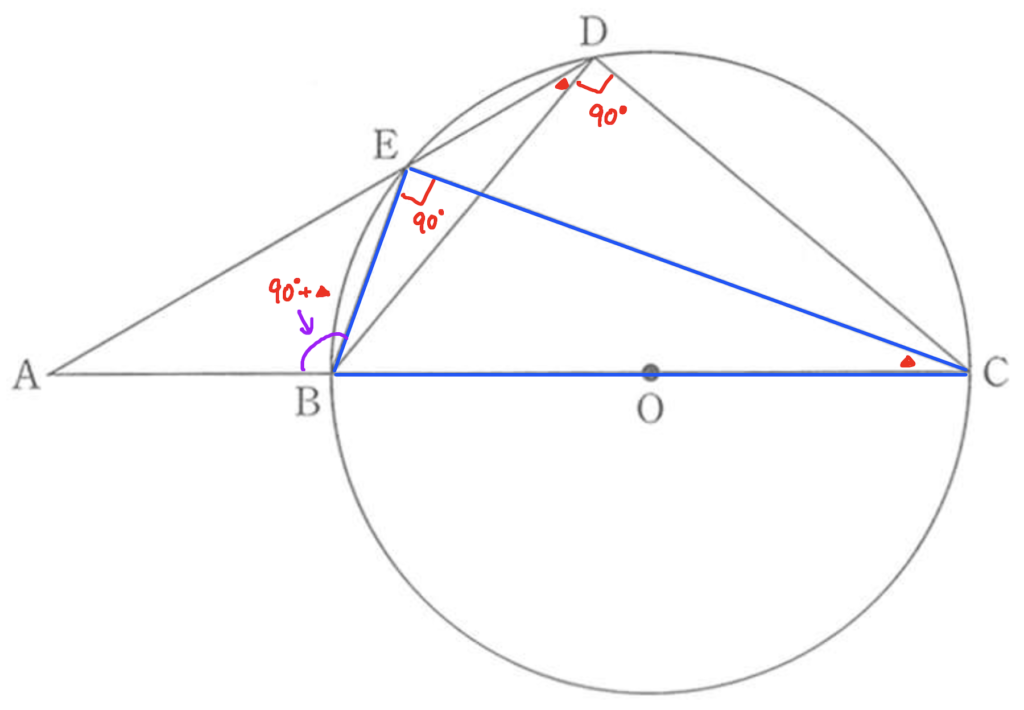
次に△EBCに注目してください。
二つの角がわかっています。
ところで、問題になっている△ABEの中で
<ABEは△EBCの中の<Bの外角になっています。
ということは、<ABEは△EBCの中の<Eと<Cを足したものということです。
つまり、<ABE = 90° + <ECBということです。
さらに、先ほど考えたように<ECBは<EDBと等しかったはずです。
以上のことから、<ABE = 90° + <EBC = 90° + <EDB = <ADCということがわかります。
すると、△AEBと△ADCにおいて
<BAE = <CAD
<ABE = <ADC
となります。
二つの角が等しいので、二つの三角形は相似であることがわかります。
証明
<BAE = <CAD ・・・ ①(共通)
<BCDと<BECは円の直径に対する円周角なので、90° ・・・ ②
<EDBと<ECBは孤EBに対する円周角なので角度は等しい ・・・③
②、③より
<ADC = 90° + <EDB
<ABEは△BECにおける<EBCの外角であるから、他の二つの角の合計と等しくなる。
よって
<ABE = <BEC + <ECB
②、③より
<ABE = 90° + <ECB = 90° + <EDB = <ADC ・・・ ⑤
以上のことから、△ABEと△ADCは二つの角が等しいので相似である。
まとめ
実際の授業では、上記の図をホワイトボードアプリを使って書きながら説明しています。
生徒さんの表情を見てホワイトボードの内容がわかったかどうかを確認して授業を進めます。
個別指導(1対1)だからできることです。
ぜひ一度体験してみてください。

