約数を求める(算数と数学の違い)
2024の約数を使う問題は2024年の入試ではよく見かけました。
今年は2023、2024。来年は2024、2025がよく出てくるのでしょう。
もちろん、受験の直前に授業で扱うとは思います。
でも、この数字だけではなくさまざまな数字の約数を求めるとき、
どのようにすればいいのでしょうか。
一つの例を解説します。
2024の素因数分解
2024を因数分解してみましょう。
2で割ると1012、さらに2で割ると506、さらに2で割ると253。
さて、253はいくつで割れるのでしょうか?
これが思い浮かぶ人は何も問題がありません。
でも、試行錯誤をして時間を浪費してしまうのも
試験としてはまずいことになるかもしれません。
では、どうすればいいのでしょうか?
2025を考える
もう少し、素因数分解をしやすい数字で考えましょう。
1増やして2025にすると考えやすいかもしれません。
2025を5で割ると405、405を5で割ると81。81は9✖︎9です。
ということは
2025 = 5 ✖︎ 5 ✖︎ 9 ✖️ 9
です。
2025は45の平方数です。
(平方数を覚えていると、このような時に役立ちます。)
ところで、
2024 = 2025 ➖ 1
です。
2025は平方数であることがわかっています。
また、1も平方数です。(1 ✖︎ 1)
ここからは数学と算数で違います。
算数の考え方
平方数は正方形の面積で表せます。
上の式は以下のように書けます。
大きな正方形の面積は45 ✖︎ 45 = 2025です。
右下の赤い正方形は1 ✖︎ 1 = 1です。
ということは、灰色の部分の面積が2025 ➖ 1 = 2024です。
ここの面積を求められればいいのです。
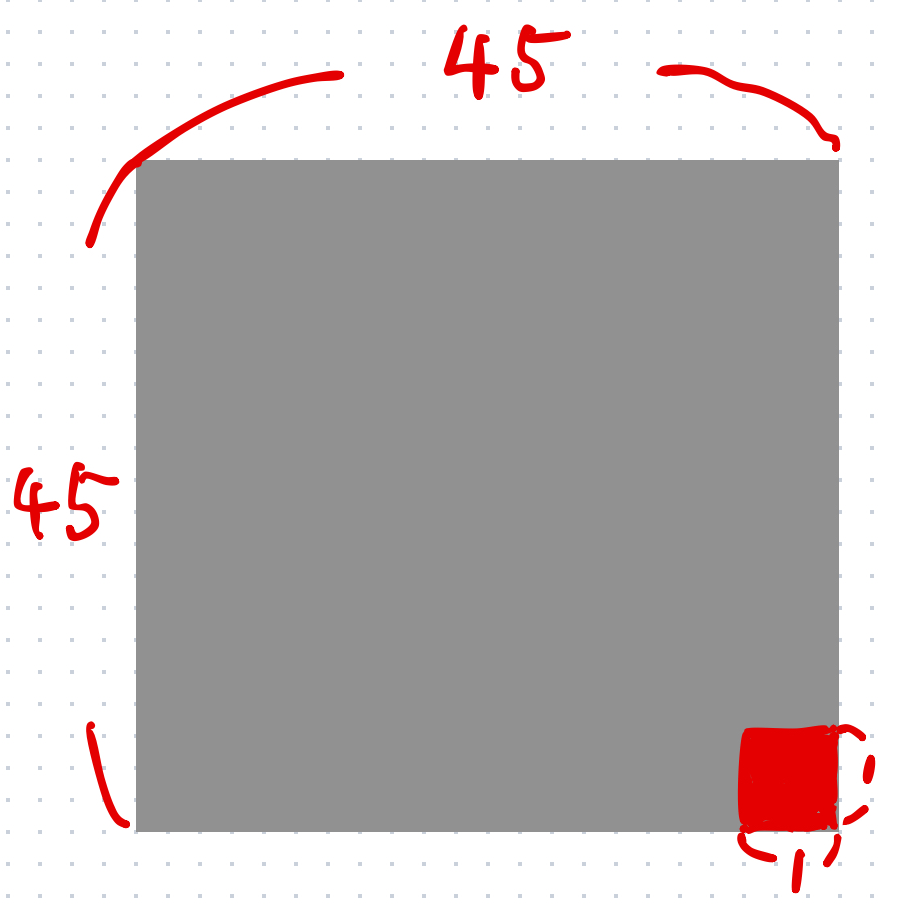
次の図を見てください。
灰色の部分は3つの部分に分けられます。
それぞれの部分の面積を求めましょう。
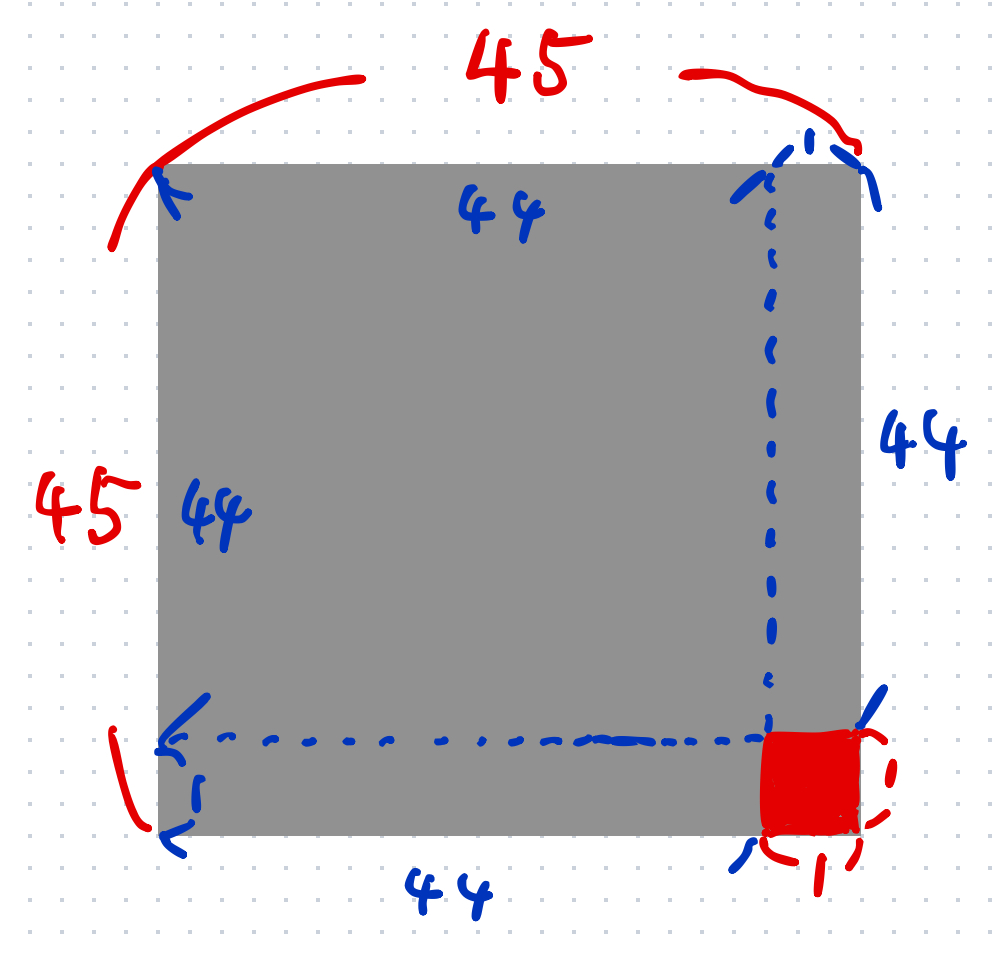
以下の図のようにしましょう。
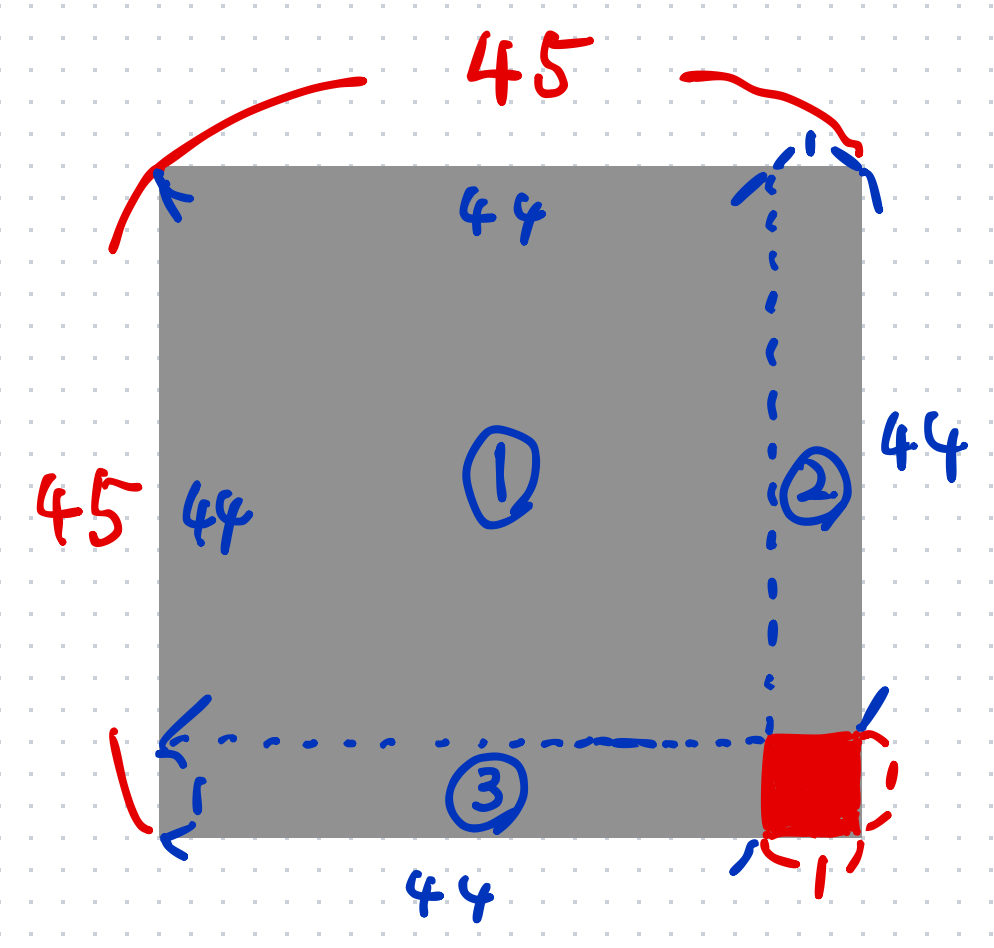
①の部分は 44 ✖︎ 44、②の部分は1 ✖︎ 44、③の部分は44 ✖︎ 1です。
つまり、
2024 = (44 ✖︎ 44) + (1 ✖︎ 44) + (1 ✖︎ 44)
となります。
これの式は全ての括弧の中に「44」があります。そこで、
2024 = 44 ✖︎ (44 + 1 + 1)
となります。
だから、
2024 = 44 ✖︎ 46
となります。
ここまできたら44と46を素因数分解しましょう。
44 = 2 ✖︎ 2 ✖︎ 11
46 = 2 ✖︎ 23
となります。
よって、
2024 = 2 ✖︎ 2 ✖︎ 11 ✖︎ 2 ✖︎ 23
となります。
数学の考え方
2024 = 2025 ➖ 1
ここで、2025を素因数分解するのは同じです。
上の内容と同じですので、
2024 = (45 ✖︎ 45) ➖ (1 ✖︎ 1)
です。
これは「二乗の差」ですね。
よって、
2024 = (45+1)(45-1) = 44 ✖︎ 46
となります。
あとは、44と46を素因数分解すればいいですね。
やっていることは、算数の時と同じです。
まとめ
算数では「掛け算の形は四角形の面積で表せる」「平方数は正方形の面積で表せる」
ということがとても大切です。
これによって図を書いて考えることができるようになります。
小学生に「和と差の積は二乗の差」を教えても、
うまく使いこなすことができないことがあります。
これは文字式なども同じですが、
小学生は「抽象化」することが苦手なのです。
その訓練をするのが数学です。
小学生でも抽象化がしっかりとできるのならば数学の解き方でも構わないと思います。
しかし、多くの場合式を立てることがうまくいかず解けなくなります。
(また、数字の範囲を指定する = 不等式も使わなければならない場合、
小学生には難易度がさらに上がります。)
また、素因数分解がうまくいかないときは
近い数字で素因数分解しやすい数字がないか考えてみましょう。
色々なテクニックを知っていることはテストの時に有利になります。
今回の内容も一つのテクニックとして知っておいて損はないと思います。



