成立学園高校　令和5年　数学より

成立学園の数学の問題を見てみましょう。

大問３を全て挙げてみました。

どのような印象を持つでしょうか？これで５点の問題が４つです。

したがって、20点。

計算や一行題が大切というのはこのようなところからも分かります。

それでは一問解いてみましょう。

成立学園数学　令和5年　大問３（１）

１から１００までの数字から連続するいくつかを取り出して足したら１００になる。このような球の取り出し方を全て探せ、という問題です。

これは等差数列の和の問題です。

等差数列の和の公式は覚えていますか？

初項がa1,最終項がanだとします。つまり、n個の項があります。このとき和は

（a1+an)×n÷2

となります。これは次のことからわかります。

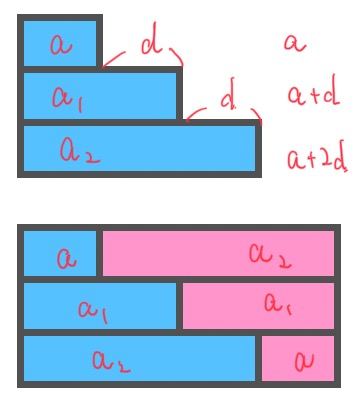
等差数列を図で表してみました。

まず上の図です。初項がa、公差がdの時、

初項a、第２項a+d、第３項a+2d

となります。

この和を求めるときにはこの図をひっくり返したものを足してあげればいいのです。

それがの上の図。

綺麗に長方形になりました。

この長方形の横の長さは初項＋最終項になります。そして、高さは項の数になります。

したがって、先ほどの公式となります。

この公式についてもう少し考えてみましょう。

初項a、最終項an、項はn個あります。

さらに、この問題の場合「連続する数」です。つまり、公差は１。

そのときにn、つまり項の数が偶数個の場合と奇数個の場合を考えてみましょう。

① 偶数個の場合

aが偶数ならanは奇数　→　a+anは奇数

aが奇数ならanは偶数　→　a+anは奇数

② 奇数個の場合

aが偶数ならanも偶数　→　a+anは偶数

aが奇数ならanも奇数　→　a+anは偶数

以上のことから、

（a1+an) が偶数の場合、nが奇数

（a1+an)が奇数の場合、nが偶数

の時に上の公式に当てはまることがわかります。

200を掛け算で表してみます。

１×200＝200

２×100＝200

４×50＝200

５×40＝100

8×25＝100

10×20＝200

これだけ考えられます。（残りはかける数とかけられる数をひっくり返しただけなので考えません）

このうち、偶数×奇数になっているのは

1×200、5×40、8×25

の３種類です。

すると、

「初項と最終項の和が200になる連続する1つの項」

「初項と最終項の和が40になる連続する５つの項」

「初項と最終項の和が25になる連続する8つの項」

が分かれば正解になります。

一つ目の文章は「連続する１つの項」はあり得ないので答えになりません。

二つ目の文章は真ん中に２０がくればいいので、

「１８、１９、２０、２１、２２」

です。

三つ目の文章は真ん中の二つが１２、１３がくればいいので

「９、１０、１１、１２、１３、１４、１５、１６」

です。

この二つが正解になります。

文章に書くと大変そうですが、等差数列の和が分かっていれば正解に辿り着けると思います。

自分で演習をしたときに、解答・解説を見て分からない！となった時、

やはり教えてもらえる環境が必要ではないでしょうか？

困ったことがあれば、当塾にご相談ください。